Racket alists vs. hashtables: which is faster when?

Sat 30 Jan 2016 12:52 EST

Tony Garnock-Jones
#racket

Joe Marshall recently measured alist vs hashtable lookup time for MIT/GNU Scheme. I thought I’d do the same for Racket.

I used a 64-bit build of Racket, version 6.3.0.3.

I ran some very quick-and-dirty informal experiments on my Acer C720 laptop, which is running a 64-bit Debian system and has 2GB RAM and a two-core Celeron 2955U at 1.40GHz.

I measured approximate alist and hash table performance for

  • fixnum keys, using eq? as the lookup predicate (so assq, hasheq) (fixnum program)
  • length-64 byte vector keys, using equal? as the lookup predicate (so assoc, hash) (byte-vector program)

Each chart below has four data series:

  • probe/alist, average time taken to search for a key that is present in an alist
  • probe/alist/missing, average time taken to search for a key that is not present in an alist
  • probe/hasheq or probe/hash, average time taken to search for a key that is present in a hash table
  • probe/hasheq/missing or probe/hasheq/missing, average time taken to search for a key that is not present in a hash table

Fixnum keys

Here are average timings for fixnum keys:

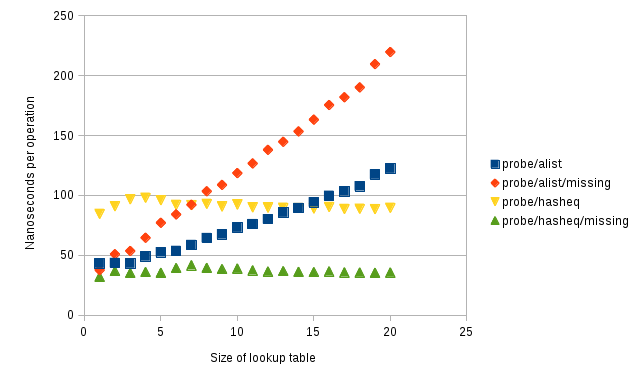
Results for fixnums and assq/hasheq

Things to note:

  • Alists are here always faster than hasheq tables for 7 keys or fewer, whether the key is present or not.

  • When the key is present in the lookup table, alists are on average faster up to around 14 keys or so.

Length-64 byte vector keys

Here are average timings for length-64 random byte vector keys:

Results for length-64 byte vectors and assoc/hash

Things to note:

  • Alists are here always faster than hasheq tables for 4 keys or fewer, whether the key is present or not.

  • When the key is present in the lookup table, alists are on average faster up to around 16 keys or so.

Conclusions

Alists will be faster when you have very few keys - for eq?, around seven or fewer, or for equal?, perhaps only as many as four, depending on the size of each key.

If you expect with high probability that a given key will be present in the table, the picture changes slightly: then, alists may be faster on average up to around perhaps fifteen keys. Specifics of the insertion order of your keys will naturally be very important in this case.

Resources

The programs I wrote:

The data I collected: