eighty-twenty

mikeb and I were discussing the papers given at BioConcur the other day, and we were puzzling out the differences between the standard way of modelling biochemical and biological reactions (including genetic interference reactions) and our “alternative” modelling style. I suppose the “alternative” style must have been tried before, and that it must display some obvious weakness we haven’t spotted yet.

Here’s a comparison of the two styles:

Join and Rates

We’ve been thinking about using a stochastic π-variant with a join operator. Having join available allows the expression of state machines to be much more direct than in a joinless stochastic π. We started modelling the lambda-switch to fit the model from this BioConcur paper, and saw that it seems more natural to attach the reaction rate to each individual join rather than to each channel as BioSPI does.

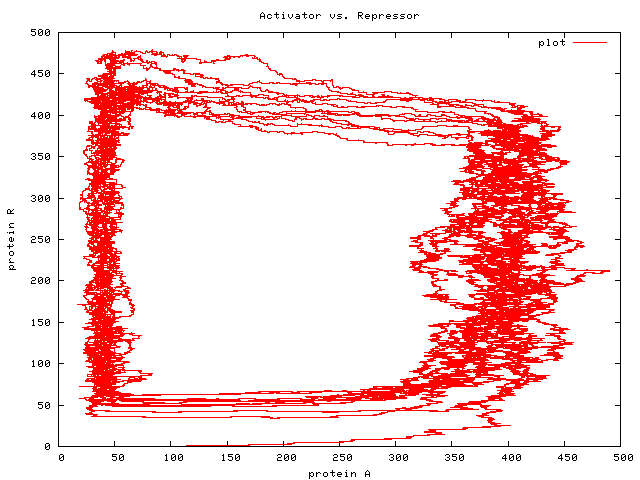
Bisimulation

The standard model has comm meaning interaction; we have comm meaning movement in some sense: atoms (mass) move from one locus (molecular species) to another, or a molecule undergoes conformational change, which is a kind of motion from one state or class or species to another. This means that bisimulation in the alternative model has to do with movement rather than interaction — which seems more fine-grained, but perhaps less natural.

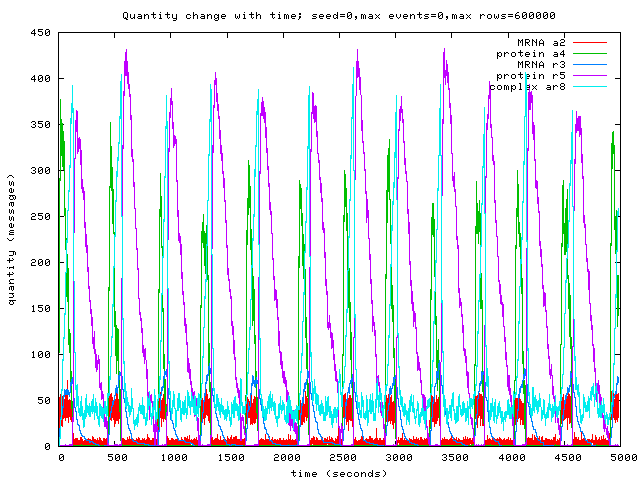
Uncertainty in Biological Simulation

We also thought about a few properties biological simulation systems ought to have. One important one is a notion of uncertainty. Few of the current systems are honest about their limits — only one of the papers at BioConcur displayed error bars on any of its graphs! The systems in use all generate probable trajectories through state-space, and this is I assume implicitly to be understood by the reader of the various program outputs, but it would be useful to have the uncertainty in the results reflected in the various displays that these systems produce.

Besides the uncertainties that come from stochastic modelling and Monte-Carlo-type approaches in general, all the inputs to the systems (eg. rates) are purely empirical data, with associated uncertainties, and these uncertainties are not propagated through the system. Not only do the outputs not show the variation in results due to random sampling, but the outputs do not explore the limits of the accuracy of the inputs, either.

Reagent concentration vs. Gillespie vs. Modelling reagent state

The alternative model deals well with high reagent concentrations, since a high concentration is modelled as a large number of messages outstanding on a channel. The Gillespie scheduling algorithms are O(n)-time in the number of enabled reactions, not in the concentrations of the reagents. The standard model suffers here because each molecule is modelled as a process — that is, as an enabled reaction. In a naïve implementation, this makes the scheduling complexity O(n)-time (or at best, O(log(n)) time if the Gibson-Bruck algorithm is used) in the number of molecules in the system.

However, modelling molecules as processes seems to provide one advantage that doesn’t easily carry over into the alternative model: molecule-processes can involve internal state that any interacting molecule need not be concerned with. For example, enzyme-private channels with different rates associated with them might be used to model the different reactivities of phosphorylated and unphosphorylated states of the enzyme.

Perhaps a hybrid of the two models will be workable; after all, even in the alternative model, you have the freedom of the restriction operator available for implementing complex behaviours. The alternative model allows some common patterns to be expressed more simply than the standard joinless model though, it seems.

We’re still thinking about ways of keeping the molecules-as-messages approach while allowing reactions to specialise on molecule-message state or to ignore it, as appropriate.

Compartments

BioSPI 3.0 took the standard stochastic-π implementation and added BioAmbients to it (see the 2003 paper by Regev, Panina, Silverman, Cardelli and Shapiro). Any stochastic-join will probably benefit from being able to model compartments similarly.

The simple, ambientless approach suffers some of the same problems as SBML is facing with regard to recognising the similarity of species across compartments. Some way of factoring out reactions/processes/etc common across all compartments should be useful.

Last week I was privileged to be able to attend some of the workshops associated with Concur 2004, a conference on Concurrency Theory. Thanks, LShift!

• On the Monday I attended BioConcur ‘04. You can find my notes under category bioconcur.

• On the Saturday I attended AVoCS ‘04. My notes are under category avocs.

(Don’t forget that, blog-style, the most recent posts are at the top, so the notes should be read upward from the bottom of each page.)

The BioConcur talks really provided some food for thought. I’m looking forward over the next few months letting some of the ideas from the conference take root, and I’ll be tracking some of the various projects with interest. It’s an exciting time to be in systems biology.

(I also caught a bit of the previous talk on semantic subtyping for π. It looks great! Also very codenameesque… anyway, to the talk at hand:)

WWW is the application considered - probabilities of event occurrences are important there (probability of, what, packet loss? server error?), as in bioambients.

The exponential distribution function is 1-e^-rt

• if you use the exp. dist. fn, you have a CTMC
• and it’s memoryless

Ambients get decorated with a parameter η which is a scaling factor, controlling the rate of reaction inside the ambient. Also actions in, out etc. get decorated with a rate just like stochastic-π.

[How does that work with bioambients? Would the η be like volume there? What happens if you try to stuff a huge ambient inside a tiny one (in bio)?]

There’s no implementation yet. This is still very preliminary work.

Precise model-checking of models with continuous state variables is difficult. DTMCs and CTMCs, discrete and continuous time Markov Chains respectively, while able to optionally model continuous time cannot model a continuous state space, having only a discrete state space. (cf. PEPA) Markovian Reward Models have a strongly limited capability for modelling continuous state — limitations include for instance that the behaviour may not depend on the continuous state variable!

Stochastic Fluid Models do better [could it be applied to the RKIP/ERK pathway problem?] at the expense of significantly more difficult analysis. Only a very small number of continuous state variable can be handled.

I missed the end — had to leave to see the stochastic-ambients talk.

This talk was about using CSP within the Balsa toolkit to model asynchronous (clock-free) hardware. Asynchronous hardware replaces the clock with explicit synchronisation using handshakes/request + acknowledgement signals.

Clockless architectures are more efficient, cheaper in transistors, and they give more opportunity for verification. They’re harder to design and designs tend to be error-prone, though. This work is focussed on the idea that verification ought to be able to offset the difficulties of working with asynchronous systems.

At sub-micron technologies, the gates are so small the manufacturing process can be inaccurate enough to cause significant differences in timing delays within the chip! Hence per-chip clock-rate limits and testing… :-/

They’re compiling a CSPish language into silicon! Cool!

• syntax-directed compilation
• doesn’t pull extra parallelism out of the code
• so writing the parallelism in is very important
• which motivates the choice of CSP

CSPish language –> “handshake network” –> gate-level network –> …

Balsa has until now been a simulation-only tool, with no verification tool available. This work is building one.

• Each interface between handshake-network components has a more-or-less session type

• Different properties are verified at different levels - some at the whole-program balsa/csp level, some at the handshake-net level, and some at the gate network level

• the top levels are synchronous models (ie. output has a continuation); lower levels are async however! so new approach used to verify async variants of csp: “protocol-based closed-circuit testing” – reminds me of behavioural type system zipper checkers! (you supply the environment and make sure it goes to zero…)

• the case study reproduced a deadlock seen in the balsa simulator, and showed positively that the fix for the problem genuinely did remove the possibility of deadlock.

• protocol at gate level is a subset of the traces of the gate net — because they have to cope with async sends at that level (?)

• standard csp semantics, standard csp model-checkers. that is the contribution - no special tools required cf. Dill and cf. Josephs

The work is using BSPA - CCS for BSP - “Bulk synchronous process algebra”. BSPA is bilevel - local level and global level. The programmer can address processors by number within a machine, but can also send messages between machines.

There are two kinds of comm: computation within the par step; and also message-sending for the global transfer step and synchronisation barrier.

The cost model is to expand individual expression to serial form (by expanding par into sum-of-sequence) and from there using “cost rules” to arrive at an expression representing the cost of the calculation. The clever step is the recognition of the semi-ring (?).

• how is she locating the barrier expressions? sync trees?

• future work: use the cost model to evaluate the need for parallel processing, whether it would help or not in specific circumstances

This talk was about a particular graph language used to describe concurrent systems. The work focussed on analysing the graphs to identify symmetry in their Kripke structures, so that the symmetry could be reduced, thereby making the model more tractable.

Notes:

• using Promela to construct models

• is constructing the entire Kripke structure the expensive bit?

• processes and channels are typed; processes and channels are coloured by type in the diagrams

• only need to consider static topology, because if there’s symmetry in the static case, then all instances of the symmetry will introduce the same patterns of new channels later on

• “automorphism group”?

Time Petri Nets introduce timing constraints on normal Petri Nets — not sharp constraints, intervals are given for each constraint.

• “boundedness” for TPNs undecidable
• “reachability” for bounded petri nets decidable
• SCG = ??
• region graph = ??
• untimed CTL* = ??
• reachability + time CTL model-checking is decidable (1994)
• so: talk on relation between the two models
• aim: structural translation; correctness proof — both achieved
• the translation permits use of existing efficient tools for analysing TAs, eg. uppaal

Future work: real case studies, perhaps with uppaal — and investigate expressiveness — can TAs be translated back to TPNs?

This talk focussed on the first experimental validation of the APMC tool. The tool was used to compute results that were then compared with results computed by PRISM.

The summary was: PRISM and APMC are complementary tools; one might use APMC to gain a feel for the solution spaces, then switch to the slower PRISM for a precise calculation, switching back to APMC when the model grows to a size intractable to PRISM’s engine. APMC is faster than PRISM, although it does only give an approximate result.

• PRISM models nondeterminism on average systems - state space explosion when the model grows

• APMC models large systems deterministically - can only handle fully probabilistic systems (?)

• This is the first real use of APMC - it is very new, developed in 2003.

• it’s a distributed model checker! They used >80 workstations

• similar kinds of questions to those that can be asked of prism

• notions of confidence - error intervals in the answers it gives you! Statistical answers - cool!

• they built a model with apmc and it has more than 10¹⁰⁰ states! (try doing that in prism).

• the results were good - apmc lined up with prism

• I noticed that the error bars were all the same in the result graphs, so I asked a question at the end - the answer was that apmc has as an engine parameter to control the size of the required confidence interval, and that the algorithm is quadratic in the required error bound (which I’m unsure what that means exactly but the general idea is clear).

This talk reported on exploring the use of CSP in implementing a Game Semantics model-checker. Traditional model checkers don’t give soundness, completeness or compositionality — but game semantics can.

Game semantics are a series of alternating “moves” between the player (P/player/program) and the opponent (O/opponent/environment). The CSP model for game semantics has channels Q and A for questions and answers respectively. The examples look like continuation-passing-style transformed parallel-functional expressions in codename — but in CSP, which is a slightly weird language.

Their system uses LTL over finite traces. They’ve implemented a compiler from a program to the CSP representation of the game semantics for the program. The language looks imperative and algol-like. The programs are compiled into a transition system; some of the input parameters controlling the size of the transition system are set ahead of time — in the examples shown, generally the size of the input was fixed at 2 (eg. a bubblesort with arraylen = 2, and a Queue ADT with size = 2). The transition diagrams look like Satnam’s butterfly diagrams!

Using CSP instead of regular expressions to model game semantics turns out to be a clear win in terms of performance.

They implemented an algorithm that finds the minimal model for a transition diagram, but while it drastically reduces the state count in the model, the algorithm itself is really slow — just using the straight model, without minimising it, turns out to be a more efficient use of resources.