Figure 1: The ring structure of a Chord-style DHT, with nodes placed around the ring.
I’ve been experimenting with Distributed Hash Tables (DHTs) recently.
A common base for DHT designs is Chord [1], where nodes place
themselves randomly onto a ring-shaped keyspace; figure 1 shows an
example.
One of the motivations of a DHT is to fairly distribute keyspace among
participating nodes. If the distribution is unbalanced, some nodes
will be doing an unfairly large amount of work, and will be storing an
unfairly large amount of data on behalf of their peers.
This post investigates exactly how unfair it can get (TL;DR:
very), and examines some options for improving the fairness of the
span distribution (TL;DR: virtual nodes kind of work).
Background: Chord-style DHTs
Chord-style DHTs map keys to values. Keys are drawn from a
k-bit key space. It’s common to imagine the whole key space,
between 0 and 2k-1, as a ring, as illustrated in figure
1.
Each node in the DHT takes responsibility for some contiguous span
of the key space. A newly-created node chooses a random number between
0 and 2k-1, and uses it as its node ID. When a node joins
the DHT, one of the first things it does is find its predecessor node.
Once it learns its predecessor’s node ID, it takes responsibility for
keys in the span (pred, self] between its predecessor’s ID and
its own ID [6].
If the keys actually in use in a particular DHT are uniformly
distributed at random, then the load on a node is directly
proportional to the fraction of the ring’s keyspace it takes
responsibility for. I’ll assume this below without further comment.
Below, I’ll use n to indicate the number of nodes in a particular
DHT ring.
Expected size of a node’s region of responsibility
My intuitions for statistics are weak, so I wrote a short and ugly
program
to experimentally explore the distribution of responsibility interval
sizes. My initial assumption (naive, I know) was that the sizes of
intervals between adjacent nodes would be normally distributed.
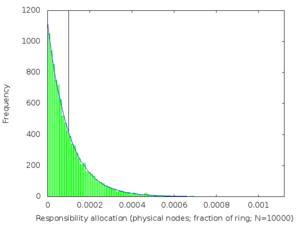
Figure 2: Distribution of distances between adjacent nodes, from a simulated 10,000-node DHT. The mean interval length, 1/10,000 = 10-4, is marked with a vertical line. The median (not marked) is 0.69×10-4: less than the mean. The blue curve is the exponential distribution with β=10-4.
I was wrong! The actual distribution, confirmed by experiment, is
exponential
(figure 2).
In an exponential distribution, the majority of intervals are shorter
than the expected length of 1/n. A few nodes are given a very unfair
share of the workload, with an interval much longer than 1/n.
How bad can it get?
The unfairness can be as bad as a factor of O(log n). For example,
in DHTs with 104 nodes, nodes have to be prepared to store
between ten and fifteen times as many key/value pairs than the mean.
How can we avoid this unfairness?
One idea is to introduce many virtual nodes per physical node: to
let a physical node take multiple spots on the ring, and hence
multiple shorter keyspace intervals of responsibility. It turns out
that this works, but at a cost.
If each physical node takes k points on the ring, we end up with
kn intervals, each of expected length 1/kn. The lengths of these
shorter intervals are exponentially distributed. Each node takes k
of them, so to figure out how much responsibility, and hence how much
load, each node will have, we need the distribution describing the sum
of the interval lengths.
An Erlang
distribution gives us exactly what we want. From Wikipedia:
[The Erlang distribution] is the distribution of the sum of k
independent exponential variables with mean μ.
We’ve already (figure 2) seen what happens when k=1. The following
table (figure 3) shows the effect of increasing k: subdividing the
ring into shorter intervals, and then taking several of them together
to be the range of keys each node is responsible for.
| k |
2 |
3 |
4 |
5 |
| Distribution |
 |
 |
 |
 |
| k |
10 |
15 |
20 |
25 |
| Distribution |
 |
 |
 |
 |
| k |
50 |
75 |
100 |
125 |
| Distribution |
 |
 |
 |
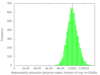 |
Figure 3. Effects of increasing
k. The green areas show results from simulation; the blue curve
overlaid on each plot is the Erlang distribution with μ=1/kn.
The mean interval length, 1/10,000, is marked with a vertical
line.
We see that the distribution of load across nodes gets fairer as k
increases, becoming closer and closer to a normal distribution with on
average 1/n of the ring allocated to each node.
The distribution gets narrower and narrower as k gets large. Once
k is large enough, we can plausibly use a normal approximation to
the Erlang distribution. This lets us estimate the standard deviation
for large k to be 1/sqrt(k) of the expected allocation size.
That is, every time we double k, the distribution only gets sqrt(2)
times tighter. Considering that the DHT’s ring maintenance protocol
involves work proportional to k, it’s clear that beyond a certain
point a high virtual-to-physical node ratio becomes prohibitive in
terms of ring maintenance costs.
Furthermore, lookups in Chord-style DHTs take O(log n) hops on
average. Increasing the number of nodes in the ring by a factor of k
makes lookup take O(log n + log k) hops.
Where do these distributions come from in the first place?
Imagine walking around the ring, clockwise from key 0. Because we
choose node IDs uniformly at random, then as we walk at a constant
rate, we have a constant probability of stumbling across a node each
step we take. This makes meeting a node on our walk a Poisson
process. Wikipedia
tells us that the exponential distribution “describes the time between
events in a Poisson process,” and that summing multiple independent
exponentially-distributed random variables gives us an Erlang
distribution, so here we are.
Conclusion
The distribution of responsibility for segments of the ring among the
nodes in a randomly-allocated Chord-style DHT is unfair, with some
nodes receiving too large an interval of keyspace.
Interval lengths in such a ring follow an exponential distribution.
Increasing the number of virtual nodes per physical node leads to load
allocation following an Erlang distribution, which improves the
situation, but only at a cost of increased ring-maintenance overhead
and more hops in key lookups.
OK, so it turns out other people have already thought all this through
I should have Googled properly for this stuff before I started
thinking about it.
A couple of easily-findable papers [2,3] mention the exponential
distribution of interval sizes. Some (e.g. [3]) even mention the gamma
distribution, which is the generalization of the Erlang distribution
to real k. There are some nice measurements of actual DHT load
closely following an exponential distribution in [4], which is a paper
on improving load balancing in Chord-style DHTs. Karger and Ruhl [5]
report on a scheme for maintaining a bunch of virtual nodes per
physical node, but avoiding the ring-maintenance overhead of doing so
by only activating one at a time.
Cassandra and its virtual nodes
Cassandra, a NoSql database using a
DHT for scalability, defaults to 256 virtual nodes (vnodes) per
physical node in recent releases. The available information (e.g.
this
and
this)
suggests this is for quicker recovery on node failure, and not
primarily for better load-balancing properties. From this
document
I gather that this is because Cassandra never used to randomly
allocate node IDs: you used to choose them up-front. New releases do
choose node IDs randomly though.
Here, they
report some experience with the new design:
However, variations of as much as 7% have been reported on small
clusters when using the num_tokens default of 256.
This isn’t so surprising, given that our Erlang distribution tells us
that choosing k=256 should yield a standard deviation of roughly
1/16 of the expected interval size.
References
[1] I. Stoica, R. Morris, D. Karger, M. F. Kaashoek, and H.
Balakrishnan, “Chord: A scalable peer-to-peer lookup service for
internet applications,” in ACM SIGCOMM, 2001.
PDF available online.
[2] H. Niedermayer, S. Rieche, K. Wehrle, and G. Carle, “On the
Distribution of Nodes in Distributed Hash Tables,” in Proc. Workshop
Peer-to-Peer-Systems and Applications (KiVS), 2005. PDF available
online.
[3] N. Xiaowen, L. Xianliang, Z. Xu, T. Hui, and L. Lin, “Load
distributions of some classic DHTs,” J. Systems Engineering and
Electronics 20(2), pp. 400–404, 2009. PDF available
online.
[4] S. Rieche, L. Petrak, and K. Wehrle. A Thermal-Dissipation-based
Approach for Balancing Data Load in Distributed Hash Tables. In Proc.
of IEEE Conference on Local Computer Networks. (LCN 2004), Tampa, FL,
USA, November 2004. PDF available
online.
[5] D. Karger and M. Ruhl, “Simple efficient load balancing
algorithms for peer-to-peer systems,” Proc. Symp. Parallelism in
Algorithms and Architectures (SPAA), 2004. PDF available
online.
[6] B. Mejías Candia, “Beernet: A Relaxed Approach to the Design of
Scalable Systems with Self-Managing Behaviour and Transactional Robust
Storage,” PhD thesis, École Polytechnique de Louvain, 2010. PDF
available online.














